The full form of LCM in Maths is the Least Common Multiple, whereas the full form of HCF is the Highest Common Factor. The H.C.F. defines the greatest factor present in between given two or more numbers, whereas L.C.M. defines the least number which is exactly divisible by two or more numbers. H.C.F. is also called the greatest common factor (GCF) and LCM is also called the Least Common Divisor.
To find H.C.F. and L.C.M., we have two important methods which are the Prime factorization method and the division method. We have learned both methods in our earlier classes. The shortcut method to find both H.C.F. and L.C.M. is a division method. Let us learn the relationship between HCF and LCM with the help of the formula here. Also, we will solve some problems based on these two concepts to understand in a better way. The article here is very helpful for primary and secondary classes students such as Class 4, Class 5, Class 6, Class 7, and Class 8.
HCF and LCM Definition
We know that the factors of a number are exact divisors of that particular number. Let’s proceed to the highest common factor (H.C.F.) and the least common multiple (L.C.M.).
HCF Definition
The full form of HCF in Maths is Highest Common Factor.
As the rules of mathematics dictate, the greatest common divisor or the gcd of two or more positive integers happens to be the largest positive integer that divides the numbers without leaving a remainder. For example, take 8 and 12. The H.C.F. of 8 and 12 will be 4 because the highest number that can divide both 8 and 12 is 4.
LCM Definition
The full form of LCM in Maths is Least Common Multiple.
In arithmetic, the least common multiple or LCM of two numbers say a and b, is denoted as LCM (a,b). And the LCM is the smallest or least positive integer that is divisible by both a and b. For example, let us take two positive integers 4 and 6.
Multiples of 4 are: 4,8,12,16,20,24…
Multiples of 6 are: 6,12,18,24….
The common multiples for 4 and 6 are 12,24,36,48…and so on. The least common multiple in that lot would be 12. Let us now try to find out the LCM of 24 and 15.

LCM of 24 and 15 = 2 × 2 × 2 × 3 × 5 = 120
More is here: Learn Mathematics
LCM of Two Numbers
Suppose there are two numbers, 8 and 12, whose LCM we need to find. Let us write the multiples of these two numbers.
8 = 16, 24, 32, 40, 48, 56, …
12 = 24, 36, 48, 60, 72, 84,…
You can see, the least common multiple or the smallest common multiple of two numbers, 8 and 12 is 24.
HCF and LCM Formula
The formula which involves both HCF and LCM is:
Say, A and B are the two numbers, then as per the formula;
A x B = H.C.F.(A, B) x L.C.M.(A, B)
We can also write the above formula in terms of HCF and LCM, such as:
H.C.F. of Two numbers = Product of Two numbers/L.C.M of two numbers
&
L.C.M of two numbers = Product of Two numbers/H.C.F. of Two numbers
NOTE- The above relation between H.C.F and L.C.M is not valid for the product of numbers greater than 2. It is only valid for the product of two numbers.
How to find HCF and LCM?
Here are the methods we can use to find the HCF and LCM of given numbers.
- Prime factorization method
- Division method
Let us learn both methods, one by one.
HCF by Prime Factorization Method
Take an example of finding the highest common factor of 144, 104 and 160.
Now let us write the prime factors of 144, 104 and 160.
144 = 2 × 2 × 2 × 2 × 3 × 3
104 = 2 × 2 × 2 × 13
160 = 2 × 2 × 2 × 2 × 2 × 5
The common factors of 144, 104 and 160 are 2 × 2 × 2 = 8
Therefore, HCF (144, 104, 160) = 8
HCF by Division Method
Steps to find the HCF of any given numbers;
The above steps can also be used to find the HCF of more than 3 numbers.
Example: Find the HCF of 144 and 160 by division method.
Since 160>144, so the dividend will be 160 and the divisor will be 144.
By using the division method, we get:
Hence, we can see here that 16 is the highest number which divides 160 and 144.
Therefore, HCF (144, 160) = 16
LCM by Prime Factorization Method
To calculate the LCM of two numbers 60 and 45. Out of other ways, one way to find the LCM of given numbers is as below:
- List the prime factors of each number first.
60 = 2 × 2 x 3 × 5
45 = 3 × 3 × 5
- Then multiply each factor the most number of times it occurs in any number.
If the same multiple occurs more than once in both the given numbers, then multiply the factor by the most number of times it occurs.
The occurrence of Numbers in the above example:
2: two times
3: two times
5: one time
LCM = 2 × 2 x 3 × 3 × 5 = 180
LCM by Division Method
Let us see with the same example, which we used to find the LCM using prime factorization.
Solve LCM of (60,45) by division method.
Therefore, LCM of 60 and 45 = 2 × 2 x 3 × 3 × 5 = 180
At BYJU’S you can also learn, Prime Factorization Of Hcf And Lcm.
HCF and LCM Examples
Example 1:
Find the Highest Common Factor of 25, 35 and 45.
Solution:
Given, three numbers as 25, 35 and 45.
We know, 25 = 5 × 5
35 = 5 × 7
45 = 5 × 9
From the above expression, we can say 5 is the only common factor for all three numbers.
Therefore, 5 is the HCF of 25, 35 and 45.
Example 2:
Find the Least Common Multiple of 36 and 44.
Solution:
Given, two numbers 36 and 44. Let us find out the LCM, by division method.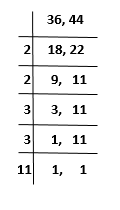
Therefore, LCM(36, 44) = 2 × 2 × 3 × 3 × 11 = 396
Example 3:
What is the L.C.M. of 25, 30, 35 and 40?
Solution:
L.C.M. of 25, 30, 35 and 40
Let us find LCM by prime factorisation.
Prime factorisation of 25 = 5 x 5 = 52
Prime factorisation of 30 = 2 x 3 x 5
Prime factorisation of 35 = 5 x 7
Prime factorisation of 40 = 2 x 2 x 2 x 5 = 23 x 5
Thus,
LCM (25, 30, 35, 40) = 2 x 2 x 2 x 3 x 5 x 5 x 7 = 4200
Example 4:
The HCF of the two numbers is 29 & their sum is 174. What are the numbers?
Solution:
Let the two numbers be 29x and 29y.
Given, 29x + 29y = 174
29(x + y) = 174
x + y = 174/29 = 6
Since x and y are co-primes, therefore, possible combinations would be (1,5), (2,4), (3,3).
The only combination that follows the co-prime part is (1,5)
For (1,5): 29 x = 29 x 1 and 29 y = 29 (5) = 145
Therefore, the required numbers are 29 and 145.
Example 5.
Find the product of two numbers whose H.C.F is 25 and L.C.M is 5.
Solution:
Product of two numbers = H.C.F x L.C.M
In this problem, the product is not possible as H.C.F given in the problem is greater than the L.C.M which is not possible.








0 Comments