Pythagoras Theorem

Pythagoras Theorem (also called Pythagorean Theorem) is an important topic in Mathematics, which explains the relation between the sides of a right-angled triangle. The sides of the right triangle are also called Pythagorean triples. The formula and proof of this theorem are explained here with examples.

Pythagoras theorem is basically used to find the length of an unknown side and the angle of a triangle. By this theorem, we can derive the base, perpendicular and hypotenuse formulas. Let us learn the mathematics of the Pythagorean theorem in detail here.

Pythagoras Theorem Statement

Pythagoras theorem states that “In a right-angled triangle,  the square of the hypotenuse side is equal to the sum of squares of the other two sides“. The sides of this triangle have been named Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle 90°. The sides of a right triangle (say a, b and c) which have positive integer values, when squared, are put into an equation, also called a Pythagorean triple.

History

The theorem is named after a Greek Mathematician called Pythagoras.

Pythagoras Theorem Formula

Consider the triangle given above:

Where “a” is the perpendicular,

“b” is the base,

“c” is the hypotenuse.

According to the definition, the Pythagoras Theorem formula is given as:

Hypotenuse2 = Perpendicular2 + Base2  c2 = a2 + b2

The side opposite to the right angle (90°)  is the longest side (known as Hypotenuse) because the side opposite to the greatest angle is the longest.

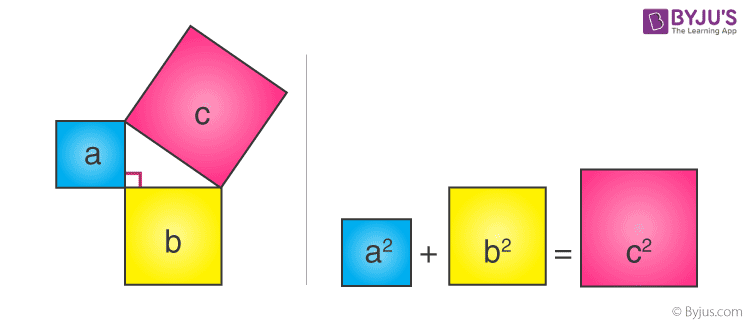
Consider three squares of sides a, b, c mounted on the three sides of a triangle having the same sides as shown.

By Pythagoras Theorem –

Area of square “a” + Area of square “b” = Area of square “c”

Example

The examples of theorem and based on the statement given for right triangles is given below:

Consider a right triangle, given below:

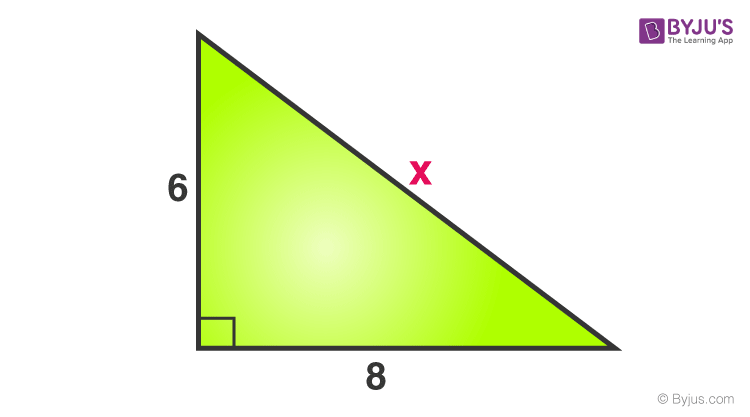
Find the value of x.

X is the side opposite to the right angle, hence it is a hypotenuse.

Now, by the theorem we know;

Hypotenuse2 = Base2 + Perpendicular2

x2 = 82 + 62

x2 = 64+36 = 100

x = √100 = 10

Therefore, the value of x is 10.

Pythagoras Theorem Proof

Given: A right-angled triangle ABC, right-angled at B.

To Prove- AC2 = AB2 + BC2

Construction: Draw a perpendicular BD meeting AC at D.

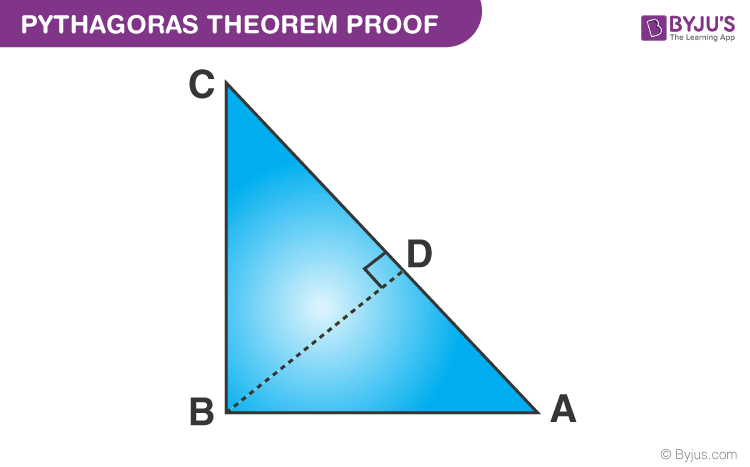
Proof:

We know, △ADB ~ △ABC

Therefore,

$\begin{array}{l}\frac{��}{��}=\frac{��}{��}\end{array}$

(corresponding sides of similar triangles)

Or, AB2 = AD × AC ……………………………..……..(1)

Also, △BDC ~△ABC

Therefore,

$\begin{array}{l}\frac{��}{��}=\frac{��}{��}\end{array}$

(corresponding sides of similar triangles)

Or, BC2= CD × AC ……………………………………..(2)

Adding the equations (1) and (2) we get,

AB2 + BC2 = AD × AC + CD × AC

AB2 + BC2 = AC (AD + CD)

Since, AD + CD = AC

Therefore, AC2 = AB2 + BC2

Hence, the Pythagorean theorem is proved.

Note: Pythagorean theorem is only applicable to Right-Angled triangle.

Applications of Pythagoras Theorem

• To know if the triangle is a right-angled triangle or not.
• In a right-angled triangle, we can calculate the length of any side if the other two sides are given.
• To find the diagonal of a square.

Useful For

Pythagoras theorem is useful to find the sides of a right-angled triangle. If we know the two sides of a right triangle, then we can find the third side.

How to use Pythagoras Theorem?

To use Pythagoras theorem, remember the formula given below:

c2 = a2 + b2

Where a, b and c are the sides of the right triangle.

For example, if the sides of a triangles are a, b and c, such that a = 3 cm, b = 4 cm and c is the hypotenuse. Find the value of c.

We know, 

c2 = a2 + b2

c2 = 32+42

c2 = 9+16

c2 = 25

c = √25

c = 5 cm

Hence, the length of hypotenuse is 5 cm.

How to find whether a triangle is a right-angled triangle?

If we are provided with the length of three sides of a triangle, then to find whether the triangle is a right-angled triangle or not, we need to use the Pythagorean theorem.

Let us understand this statement with the help of an example.

Suppose a triangle with sides 10cm, 24cm, and 26cm are given. 

Clearly, 26 is the longest side.

It also satisfies the condition, 10 + 24 > 26

We know,

c2 = a2 + b2    ………(1)

So, let a = 10, b = 24 and c = 26

First we will solve R.H.S. of equation 1.

a2 + b2 = 102 + 242 = 100 + 576 = 676

Now, taking L.H.S, we get;

c2 = 262 = 676

We can see, 

LHS = RHS

Therefore, the given triangle is a right triangle, as it satisfies the Pythagoras theorem.

Pythagorean Theorem Solved Examples

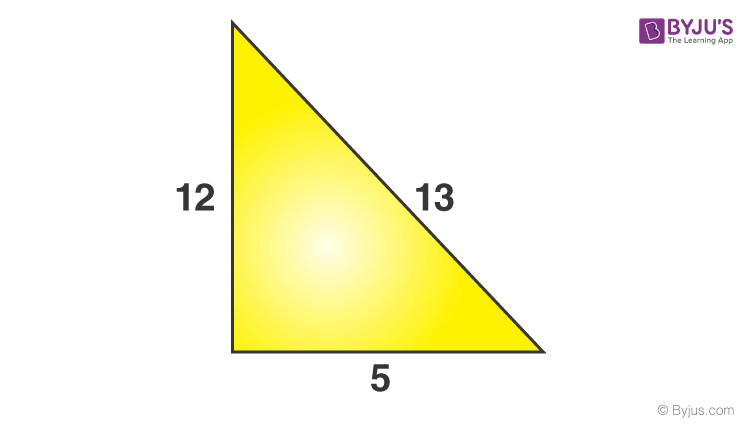
Problem 1: The sides of a triangle are 5, 12 & 13 units. Check if it has a right angle or not.

Solution: From Pythagoras Theorem, we have;

Perpendicular2 + Base2 = Hypotenuse2

P2 + B2 = H2

Let,

Perpendicular (P) = 12 units

Base (B)= 5 units

Hypotenuse (H) = 13 units {since it is the longest side measure}

LHS = P2 + B2

⇒ 122 + 52

⇒ 144 + 25

⇒ 169

RHS = H2

⇒ 132

⇒ 169

⇒ 169 = 169 

L.H.S. = R.H.S.

Therefore, the angle opposite to the 13 units side will be a right angle.

Problem 2: The two sides of a right-angled triangle are given as shown in the figure. Find the third side.

Solution: Given;

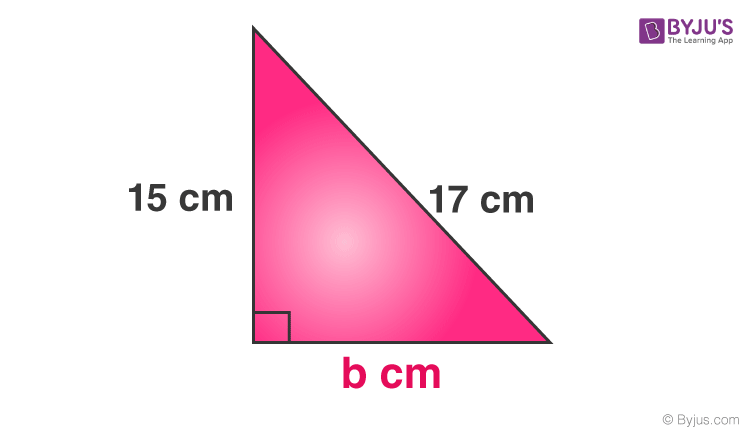
Perpendicular = 15 cm

Base = b cm

Hypotenuse = 17 cm

As per the Pythagorean Theorem, we have;

Perpendicular2 + Base2 = Hypotenuse2

⇒152 + b2 = 172

⇒225 + b2 = 289

⇒b2 = 289 – 225

⇒b2 = 64

⇒b = √64

Therefore, b = 8 cm

Problem 3: Given the side of a square to be 4 cm. Find the length of the diagonal.

Solution- Given;

Sides of a square = 4 cm

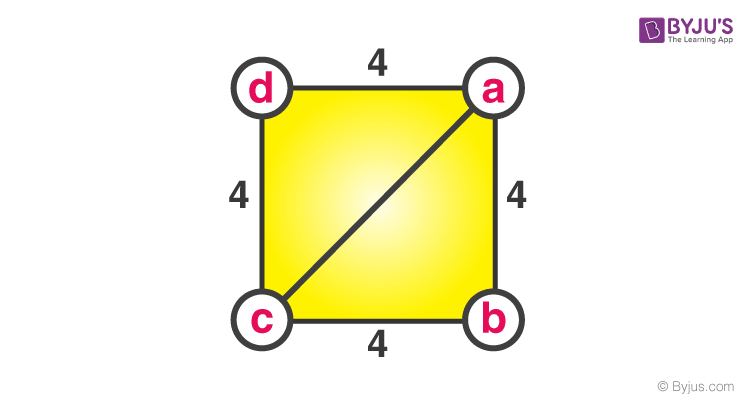
To Find- The length of diagonal ac.

Consider triangle abc (or can also be acd)

(ab)2 +(bc)2 = (ac)2

(4)2 +(4)2= (ac)2

16 + 16 = (ac)2

32 = (ac)2

(ac)2 = 32

ac = 4√2.

Thus, the length of the diagonal is 4√2 cm.