Pentagon

A pentagon is a geometrical shape, which has five sides and five angles. Here, “Penta” denotes five and “gon” denotes angle. The pentagon is one of the types of polygons. The sum of all the interior angles for a regular pentagon is 540 degrees.

In Geometry, we study about different types of shapes. The two-dimensional shape that is composed of straight lines and interior angles is known as a polygon. The examples of polygons are:

• Triangle (three-sided polygon)
• Quadrilateral (four-sided polygon)
• Pentagon (five-sided polygon)
• Hexagon (six-sided polygon)
• Heptagon (seven-sided polygon)
• Octagon (eight-sided polygon) and so on.

In this article, you can learn about the five-sided polygon called “pentagon” with proper definition, shape, sides, properties along with its perimeter and area of a pentagon formula in detail.

Pentagon Definition

A pentagon is a polygon with 5 sides and 5 angles. The word “pentagon” is made up of two words, namely Penta and Gonia, which means five angles. All the sides of a pentagon meet with each other end to end to form a shape. Therefore,

The number of sides of a pentagon = 5

Pentagon shape

Like other polygons such as triangle, quadrilaterals, square, rectangle, etc., the pentagon is also a polygon that contains five sides and five angles.

Depending on the sides, angles, and vertices, there are different types of pentagon shapes, such as

• Regular and Irregular pentagon
• Convex and Concave pentagon

Regular and Irregular Pentagon

If a pentagon is regular, then all the sides are equal in length, and five angles are of equal measures. If the pentagon does not have equal side length and angle measure, then it is known as an irregular pentagon.

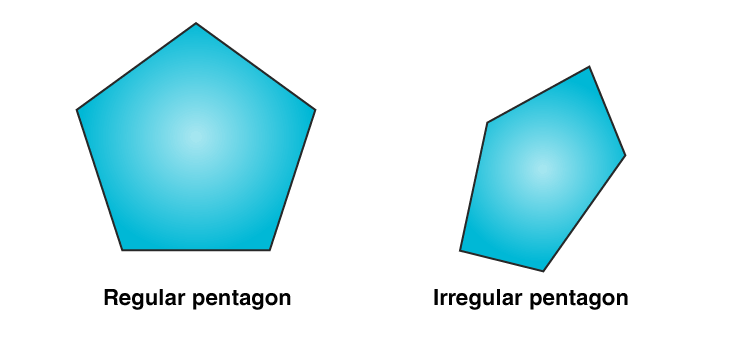
Regular Pentagon

As defined above, a regular pentagon contains five congruent sides. Thus, we can easily find the perimeter of this type of pentagon. This can be observed from the below given figure.

Here, all the five sides are equal so the perimeter of a regular pentagon is five times the length of any one of its sides.

Also, we can divide a regular pentagon into five similar triangles as shown below.

Thus, we can say that the area of a regular pentagon is equal to the 5 times area of a triangle with sides the same as the pentagon.

Convex and Concave Pentagon

If all the vertices of a pentagon are pointing outwards, it is known as a convex pentagon. If a pentagon has at least one vertex pointing inside, then the pentagon is known as a concave pentagon.

Pentagon Properties

Some properties of the pentagon are as follows:

• In the pentagon, the sum of the interior angles is equal to 540°.
• If all the sides are equal and all the angles are of equal measure, then it is a regular pentagon. Otherwise, it is irregular.
• In the regular pentagon, each interior angle measures 108°, and each exterior angle measures 72°.
• An equilateral pentagon has 5 equal sides.
• The sum of the interior angles of a rectangular pentagon is 540°.

Area of a Pentagon

For a regular pentagon with side and apothem length, then the formula to find the area of a pentagon is given as

Area of a Pentagon, A = (5/2) × Side Length × Apothem square units

If only the side length of a pentagon is given, then

Area = 5s2 / (4 tan 36°) Square units

If only the radius of a pentagon is given, then

Area =(5/2)r2 sin 72° Square units

Perimeter of Pentagon

Since all the sides “a” of a regular pentagon are of equal measure, then the perimeter or circumference of a pentagon is written as,

The perimeter of a pentagon, P = 5a units

Pentagon Solved problem

Question: Find the area and perimeter of a regular pentagon whose side is 5 cm and apothem length is 6 cm.

Solution:

Given:

The side of a pentagon, a = 5 cm

Apothem Length = 6 cm

We know that

The area of a pentagon, A = (5/2) ×Side Length ×Apothem square units

Substitute side = 5 cm, Apothem = 6 cm in formula,

A = (5/2) × 5 × 6

A = 5 × 5 × 3

A = 75

Therefore, the area of a pentagon is 75 cm2

The perimeter of a pentagon, P = 5a units

P = 5(5)

P = 25 cm

Hence, the perimeter of a pentagon is 25 cm.

Based on the properties of pentagons, there are other types of pentagons that exist in geometry. They are:

1. Equilateral pentagon

A polygon with five sides of equal length is called an equilateral pentagon. However, all the five internal angles of a pentagon can take a range of sets of values. They are thus allowing it to form a family of pentagons. Therefore, the regular pentagon is unique up to similarity. Because it is an equilateral and equiangular (since its five angles are equal) pentagon.

2. Cyclic pentagon

If all the vertices of a pentagon lie on the circumference of a circle, then it is called a cyclic pentagon. The regular pentagon is the best example of a cyclic pentagon. The area of a cyclic pentagon can be represented as one fourth the square root of one of the roots of a septic equation. Here, the coefficients of the equation are functions of the sides of the pentagon. This applies to both regular and irregular pentagons.

Line of Symmetry of a Pentagon:

When coming to the line symmetry, every polygon has a certain number of lines of symmetry. For example, a square has 4 lines of symmetry. In the same way, a regular pentagon has 5 lines of symmetry.

&

Win