Segment and area of a segment of the circle

Segment and Area of a Segment Of Circle

Segment and area of a segment of the circle: A segment is a part of a circle basically the region between the chord and an arc. A circle is a path traced by a point that is equidistant from a unique point on the plane, this point is called the centre of the circle and the constant distance is called the radius of the circle. A segment is an interior region of a circle. The area enclosed by a segment and the angle subtended by a segment is called a sector. The area of the segment of a circle is determined by subtracting the triangle formed inside the sector from the sector which has the segment. 

In this article, we shall discuss in detail the segment and area of a segment of a circle and all related theorems with proof.

Segment of a Circle Definition

A segment of a circle can be defined as a region bounded by a chord and a corresponding arc lying between the chord’s endpoints. In other words, a circular segment is a region of a circle which is created by breaking apart from the rest of the circle through a secant or a chord. We can also define segments as the parts that are divided by the circle’s arc and connected through a chord by the endpoints of the arc. It is to be noted that the segments do not contain the center point.

Types of Segments in a Circle

According to the definition, the part of the circular region which is enclosed between a chord and corresponding arc is known as a segment of the circle. There are two classifications of segments in a circle, namely the major segment and the minor segment. The segment having a larger area is known as the major segment and the segment having a smaller area is known as the minor segment.

In the figure above, ADB is the major segment and ABC is the minor segment. If nothing is stated, a segment means the minor segment. In order to calculate the area of a segment of a circle, one should know how to calculate the area of the sector of the circle.

Area of a Segment of a Circle Formula

The formula to find segment area can be either in terms of radians or in terms of degree. The formulas for a circle’s segment are as follows:

Area of a Segment of a Circle Formula

Formula To Calculate Area of a Segment of a Circle
Area of a Segment in Radians	A = (½) × r2 (θ – Sin θ)
Area of a Segment in Degrees	A = (½) × r 2 × [(π/180) θ – sin θ]

How to Calculate the Area of Segment of Circle?

Figure 1: Segment of a Circle Derivation

In fig. 1, if ∠AOB = θ (in degrees), then the area of the sector AOBC (A sector AOBC) is given by the formula;

(A sector AOBC) = θ/360° × πr2

Let the area of ΔAOB be AΔAOB. So, the area of the segment ABC(A segment ABC) is given by

(A segment ABC) = (A sector AOBC) – AΔAOB

(A segment ABC) = θ/360° × πr2 – AΔAOB

Figure 2: Calculating Area of Segment of Circle

The area of ΔAOB can be calculated in two steps, As shown in fig. 2,

Calculate the height of ΔAOB i.e. OP using Pythagoras theorem as given below:

OP = √[r2–(AB/2)2] if the length of AB is given

or, OP = r cos (θ/2), if θ is given (in degrees)

Calculate the area of ∆AOB using the formula:

(A area ΔAOB) = ½ × base × height = ½ × AB × OP

Now, substituting the values in the area of segment formula, the area can be calculated.

Theorems on Segment of a Circle

There are two main theorems based on a circle’s segments which are:

• Alternate Segment Theorem
• Angle in the Same Segment Theorem
• Alternate Angle Theorem

Theorem 1: Inscribed Angle Theorem

Statement: The inscribed angle theorem states that an angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc on the circle.

In the below figure, ∠AOC = 2∠ABC

Inscribed Angle Theorem

Proof:

Consider the alternate angle ACD (as x) is equal to the angle ABC is shown on the other side of the chord, where DC is the tangent to the circle.

Triangle ABC has points A, B and C on the circumference of a circle with centre O. Join OA and OC to form triangle AOC.

Let ∠ACD = x, and ∠OCA = y.

We know that tangent to a circle is at a right angle to the radius of a circle,

Therefore, x + y = 90° ——————————(i)

Bisect the triangle AOC from the point O, then the triangle formed is a right-angled triangle at E. Let the bisected angle be z.

Therefore, ∠AOE = ∠COE =z

Sum of angles of a triangle is 180°

In △COE, y + z + 90° = 180°

Or, y + z = 90° —————————(ii)

Equating equation (i) and (ii), we have

x = z

We know, ∠ABC = ∠ACD = x

Therefore, ∠AOC = 2z

and ∠ABC = x

Which implies ∠AOC = 2∠ABC

Theorem 2: Angle in the Same Segment Theorem

Statement: Angles which are in the same segment are equal, i.e. angles subtended (made) by the same arc at the circumference are equal.

According to angle in the same segment theorem, angles in the same segment are equal. Consider triangle ABC and ADC having ∠ABC and ∠ADC in the major segment of a circle.

To prove: ∠ABC = ∠ADC

Construction: Join O to A and C.

Angles in Same Segment Theorem

Proof:

Let ∠AOC = x

From Theorem 1, we have

x = 2∠ABC —————–(i)

Also, x = 2∠ADC ———————-(ii)

From (i) and (ii), we have

∠ABC = ∠ADC

Theorem 3: Alternate Angle Theorem

Statement: The alternate segment theorem (also known as the tangent-chord theorem) states that in any circle, the angle between a chord and a tangent through one of the endpoints of the chord is equal to the angle in the alternate segment.

In the following figure, ∠ACD = ∠ABC = x

Alternate Angle Theorem

Example Question Based on Segment Formula

Question 1: 

What is the area of the segment corresponding to the arc subtending an angle of 60° at the centre of a circle with radius 6 cm?

Solution:

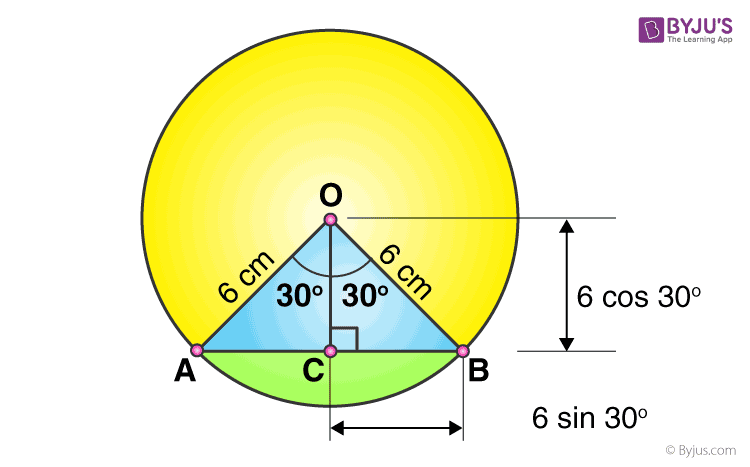
Area of the sector AOB (blue region + green region) = (θ/360°) × πr2 = (60°/360°) × π × 62 = 6π cm2

Area of ΔAOB = ½ × OC × AB

Where OC = 6 cos 30° = 6 × (√3/2) = 3√3 cm

And AB = 2BC = 2 × 6 sin 30° = 2 × 6 × ½ = 6 cm

Substituting the values, Area of ∆AOB = ½ × 3√3 × 6 = 9√3 cm2

So, area of segment AB = 6π cm2 – 9√3 cm2

= 3(2π – 3√3) cm2

&

Win