An object is said to be accelerated if there is a change in its velocity. The change in the velocity of an object could be an increase or decrease in speed or a change in the direction of motion. A few examples of acceleration are the falling of an apple, the moon orbiting around the earth, or when a car is stopped at the traffic lights. Through these examples, we can understand that when there is a change in the direction of a moving object or an increase or decrease in speed, acceleration occurs.
What Is Acceleration?
Acceleration is defined as
The rate of change of velocity with respect to time.
Acceleration is a vector quantity as it has both magnitude and direction. It is also the second derivative of position with respect to time or it is the first derivative of velocity with respect to time.
Acceleration Formula
One may have perceived that pushing a terminally ill bus can give it a sudden start. That’s because lift provides an upward push when it starts. Here velocity changes and this is acceleration! Henceforth, the frame accelerates. Acceleration is described as the rate of change of velocity of an object. A body’s acceleration is the final result of all the forces being applied to the body, as defined by Newton’s second law. Acceleration is a vector quantity that is described as the frequency at which a body’s velocity changes.
One may have perceived that pushing a terminally ill bus can give it a sudden start. That’s because lift provides an upward push when it starts. Here velocity changes and this is acceleration! Henceforth, the frame accelerates. Acceleration is described as the rate of change of velocity of an object. A body’s acceleration is the final result of all the forces being applied to the body, as defined by Newton’s second law. Acceleration is a vector quantity that is described as the frequency at which a body’s velocity changes.
Formula of Acceleration
Acceleration is the rate of change in velocity to the change in time. It is denoted by symbol a and is articulated as-
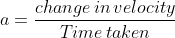
The S.I unit for acceleration is meter per second square or m/s2.
If t (time taken), v (final velocity) and u (initial velocity) are provided. Then the acceleration is given by the formula
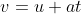
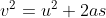
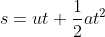
Where,
- Final Velocity is v
- Initial velocity is u
- Acceleration is a
- Time taken is t
- Distance traveled is s
Acceleration is the rate of change in velocity to the change in time. It is denoted by symbol a and is articulated as-
The S.I unit for acceleration is meter per second square or m/s2.
If t (time taken), v (final velocity) and u (initial velocity) are provided. Then the acceleration is given by the formula
Where,
- Final Velocity is v
- Initial velocity is u
- Acceleration is a
- Time taken is t
- Distance traveled is s
Where,
- a is the acceleration in m.s-2
- vf is the final velocity in m.s-1
- vi is the initial velocity in m.s-1
- t is the time interval in s
- Δv is the small change in the velocity in m.s-1
What Is the Unit of Acceleration?
The SI unit of acceleration is given as:
Types of Acceleration

Uniform and Non-uniform Acceleration
So can we have a situation when speed remains constant but the body is accelerated? Actually, it is possible in a circle where speed remains constant but since the direction is changing hence the velocity changes, and the body is said to be accelerated.
Average Acceleration
The average acceleration over a period of time is defined as the total change in velocity in the given interval divided by the total time taken for the change. For a given interval of time, it is denoted as ā.
Mathematically,
Where v2 and v1 are the instantaneous velocities at time t2 and t1 and ā is the average acceleration.
What Is Instantaneous Acceleration?
Instantaneous acceleration is defined as
The ratio of change in velocity during a given time interval such that the time interval goes to zero.
Velocity-Time Graph

Average acceleration: In the velocity-time graph shown above, the slope of the line between the time interval t1 and t2 gives the average value for the rate of change of velocity for the object during the time t1 and t2.
Instantaneous acceleration: In a velocity-time curve, the instantaneous acceleration is given by the slope of the tangent on the v-t curve at any instant.

Positive, Negative and Zero Acceleration

Consider the velocity-time graph shown above. Here, between the time intervals of 0-2 seconds, the velocity of the particle is increasing with respect to time; hence the body is experiencing a positive acceleration as the slope of the v-t curve in this time interval is positive.
Between the time intervals of 2-3 seconds, the velocity of the object is constant with respect to time; hence the body is experiencing zero acceleration as the slope of the v-t curve in this time interval is 0.
Now, between the time intervals of 3-5 seconds, the velocity of the body is decreasing with respect to time; hence the body experiences a negative value of the rate of change of velocity as the slope of the v-t curve in this time interval is negative.
Acceleration Solved Examples
Underneath we have provided some sample numerical based on acceleration which might aid you to get an idea of how the formula is made use of:
Problem 1: A toy car accelerates from 3 m/s to 5 m/s in 5 s. What is its acceleration?
Answer:
Given: Initial Velocity u = 3 m/s,
Final Velocity v = 5m/s,
Time taken t = 5s.
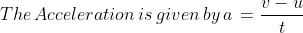
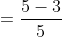
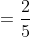
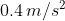
Problem 2: A stone is released into the river from a bridge. It takes 4s for the stone to touch the river’s water surface. Compute the height of the bridge from the water level.
Answer:
(Initial Velocity) u = 0 (because the stone was at rest),
t = 4s (t is Time taken)
a = g = 9.8 m/s2, (a is Acceleration due to gravity)
distance traveled by stone = Height of bridge = s
The distance covered is articulated by
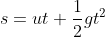
s = 0 + 1/2 × 9.8 × 4 = 19.6 m/s2
Therefore, s = 19.6 m/s2
Underneath we have provided some sample numerical based on acceleration which might aid you to get an idea of how the formula is made use of:
Problem 1: A toy car accelerates from 3 m/s to 5 m/s in 5 s. What is its acceleration?
Answer:
Given: Initial Velocity u = 3 m/s,
Final Velocity v = 5m/s,
Time taken t = 5s.
Problem 2: A stone is released into the river from a bridge. It takes 4s for the stone to touch the river’s water surface. Compute the height of the bridge from the water level.
Answer:
(Initial Velocity) u = 0 (because the stone was at rest),
t = 4s (t is Time taken)
a = g = 9.8 m/s2, (a is Acceleration due to gravity)
distance traveled by stone = Height of bridge = s
The distance covered is articulated by
s = 0 + 1/2 × 9.8 × 4 = 19.6 m/s2
Therefore, s = 19.6 m/s2
Q1. What will be the acceleration of an object which moves with uniform velocity?
Ans: Given,
The velocity is uniform, therefore the initial and final velocities are equal and is given as V.
∴From definition, acceleration is given as:
Q2. A truck is moving with a constant velocity, v = 5 m.s-1. The driver stops for diesel and the truck accelerates forward. After 20 seconds, the driver stops accelerating to maintain a constant velocity, v = 25 m.s-1. What is the truck’s acceleration?
Ans: Given,
Initial velocity, vi = 5 m.s-1
Final velocity, vf = 25 m.s-1
Time interval, t = 20 s
∴ By the definition, acceleration is given as:
Q3. Find the final velocity of the ball that is dropped from the second floor if the ball takes 18 seconds before hitting the ground. The acceleration due to gravity is g = 9.80 m.s-2.
Ans: Given,
Initial velocity, vi = 0 m.s-1
Final velocity, vf = ?
Acceleration due to gravity = a = g = 9.80 m.s-2
Time interval, t = 18 s
∴ From the definition, acceleration is given as:
vf=vi + at
vf= 0+(9.80×18)
vf=176.4 m.s-1
What Is the Difference between Acceleration and Velocity?
Following is the table of acceleration vs velocity:








0 Comments