Conic Sections

Conic sections are one of the important topics in Geometry. There are different types of conic sections in maths that can be defined based on the angle formed between the plane and intersection of the right circular cone with it. 

What are Conic Sections

A curve, generated by intersecting a right circular cone with a plane is termed as ‘conic’. It has distinguished properties in Euclidean geometry. The vertex of the cone divides it into two nappes referred to as the upper nappe and the lower nappe.

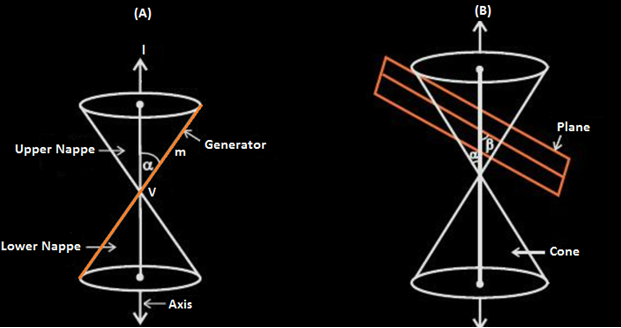
In figure B, the cone is intersected by a plane and the section so obtained is known as a conic section. Depending upon the position of the plane which intersects the cone and the angle of intersection β, different types of conic sections are obtained. Namely;

• Circle
• Ellipse
• Parabola
• Hyperbola

The rear mirrors you see in your car or the huge round silver ones you encounter at a metro station are examples of curves. Curves have huge applications everywhere, be it the study of planetary motion, the design of telescopes, satellites, reflectors etc. Conic consist of curves which are obtained upon the intersection of a plane with a double-napped right circular cone. Let us discuss the formation of different sections of the cone, formulas and their significance.

Conic Section Formulas

Check the formulas for different types of sections of a cone in the table given here.

Circle	(x−a)2+(y−b)2=r2	Center is (a,b) Radius is r
Ellipse with the horizontal major axis	(x−a)2/h2+(y−b)2/k2=1	Center is (a, b) Length of the major axis is 2h. Length of the minor axis is 2k. Distance between the centre and either focus is c with c2=h2−k2, h>k>0
Ellipse with the vertical major axis	(x−a)2/k2+(y−b)2/h2=1	Center is (a, b) Length of the major axis is 2h. Length of the minor axis is 2k. Distance between the centre and either focus is c with c2=h2−k2, h>k>0
Hyperbola with the horizontal transverse axis	(x−a)2/h2−(y−b)2/k2=1	Center is (a,b) Distance between the vertices is 2h Distance between the foci is 2k. c2=h2  + k2
Hyperbola with the vertical transverse axis	(x−a)2/k2−(y−b)2/h2=1	Center is (a,b) Distance between the vertices is 2h Distance between the foci is 2k. c2= h2  + k2
Parabola with the horizontal axis	(y−b)2=4p(x−a), p≠0	Vertex is (a,b) Focus is (a+p,b) Directrix is the line x=a−p Axis is the line y=b
Parabola with vertical axis	(x−a)2=4p(y−b), p≠0	Vertex is (a,b) Focus is (a+p,b) Directrix is the line x=b−p Axis is the line x=a

Focus, Eccentricity and Directrix of Conic

A conic section can also be described as the locus of a point P moving in the plane of a fixed point F known as focus (F) and a fixed line d known as directrix (with the focus not on d) in such a way that the ratio of the distance of point P from focus F to its distance from d is a constant e known as eccentricity. Now,

• If eccentricity, e = 0, the conic is a circle
• If 0<e<1, the conic is an ellipse
• If e=1, the conic is a parabola
• And if e>1, it is a hyperbola

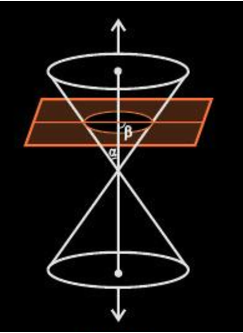
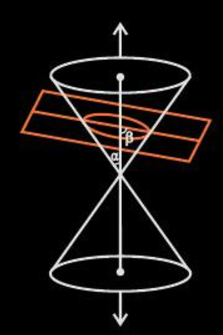
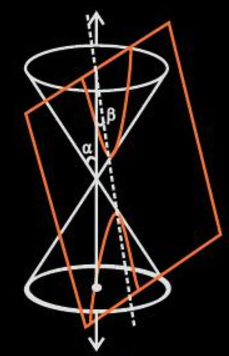
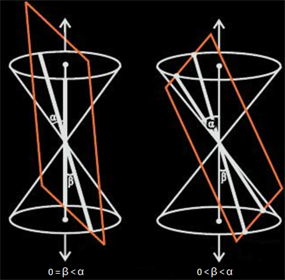
So, eccentricity is a measure of the deviation of the ellipse from being circular. Suppose, the angle formed between the surface of the cone and its axis is β and the angle formed between the cutting plane and the axis is α, the eccentricity is;

e = cos α/cos β

Parameters of Conic

Apart from focus, eccentricity and directrix, there are few more parameters defined under conic sections.

• Principal Axis: Line joining the two focal points or foci of ellipse or hyperbola. Its midpoint is the centre of the curve.
• Linear Eccentricity: Distance between the focus and centre of a section.
• Latus Rectum: A chord of section parallel to directrix, which passes through a focus.
• Focal Parameter: Distance from focus to the corresponding directrix.
• Major axis: Chord joining the two vertices. It is the longest chord of an ellipse.
• Minor axis: Shortest chord of an ellipse.

Sections of the Cone

Consider a fixed vertical line ‘l’ and another line ‘m’ inclined at an angle ‘α’ intersecting ‘l’ at point V as shown below:

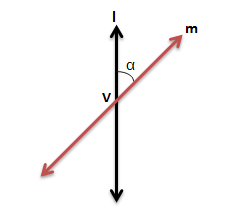
The initials as mentioned in the above figure A carry the following meanings:

1. V is the vertex of the cone
2. l is the axis of the cone
3. m, the rotating line the is a generator of the cone

Let us briefly discuss the different conic sections formed when the plane cuts the nappes (excluding the vertex).

Conic Section Circle

If β=90o, the conic section formed is a circle as shown below.

Conic Section Ellipse

If α<β<90o, the conic section so formed is an ellipse as shown in the figure below.

Conic Section Parabola

If α=β, the conic section formed is a parabola (represented by the orange curve) as shown below.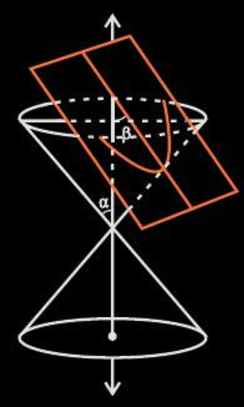

Conic Section Hyperbola

If 0≤β<α, then the plane intersects both nappes and the conic section so formed is known as a hyperbola (represented by the orange curves).

Conic Section Standard Forms

After the introduction of Cartesian coordinates, the focus-directrix property can be utilised to write the equations provided by the points of the conic section. When the coordinates are changed along with the rotation and translation of axes, we can put these equations into standard forms. For ellipses and hyperbolas, the standard form has the x-axis as the principal axis and the origin (0,0) as the centre. The vertices are (±a, 0) and the foci (±c, 0). Define b by the equations c2= a2 − b2 for an ellipse and c2 = a2 + b2 for a hyperbola.

For a circle, c = 0 so a2 = b2. For the parabola, the standard form has the focus on the x-axis at the point (a, 0) and the directrix is the line with equation x = −a. In standard form, the parabola will always pass through the origin.

• Circle: x2+y2=a2
• Ellipse: x2/a2 + y2/b2 = 1
• Hyperbola: x2/a2 – y2/b2 = 1
• Parabola: y2=4ax when a>0

Conic Sections Examples

If the plane intersects exactly at the vertex of the cone, the following cases may arise:

• If α< β≤90°, then the plane intersects the vertex exactly at a point.

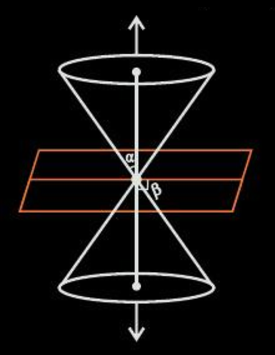
• If α=β, the plane upon an intersection with a cone forms a straight line containing a generator of the cone. This condition is a degenerated form of a parabola.

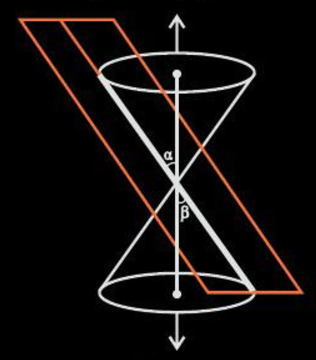
• If 0≤β<α, the section formed is a pair of intersecting straight lines. This condition is a degenerated form of a hyperbola.

Conic Sections Equations

Conic section Name	Equation when the centre is at the Origin, i.e. (0, 0)	Equation when centre is (h, k)
Circle	x2 + y2 = r2; r is the radius	(x – h)2 + (y – k)2 = r2; r is the radius
Ellipse	(x2/a2) + (y2/b2) = 1	(x – h)2/a2 + (y – k)2/b2 = 1
Hyperbola	(x2/a2) – (y2/b2) = 1	(x – h)2/a2 – (y – k)2/b2 = 1
Parabola	y2 = 4ax, where a is the distance from the origin to the focus

Solved Questions on Conic Sections

Question 1:

Find the coordinates of the focus and the vertex, the equations of the directrix and the axis, and the length of the latus rectum of the parabola y2 = 8x.

Solution:

Comparing the given equation of parabola to the standard form y2 = 4ax, we get a = 2. Thus,

Coordinates of focus	F( a, 0), that is, F(2, 0)
Coordinates of vertex	O(0, 0)
Equation of Directrix	x = –a, that is, x = –2
Equation of axis	Its axis is x-axis whose equation is y = 0
Length of latus rectum	4a, that is, 4 × 2 = 8 units

Question 2:

Given an ellipse whose foci are at (±4, 0) and the eccentricity is ⅓. Find the equation of the ellipse.

Solution:

By the coordinates of focus, we get that the ellipse is a horizontal ellipse whose major axis lies on the x-axis. 

Let the equation of the ellipse be

x2/a2 + y2/b2 = 1, where a2 > b2

For an ellipse, the eccentricity e = c/a ⇒ a = c/e where (±c, 0) is the focus

∴ a = 4/(⅓ ) = 12.

Now, c2 = (a2 – b2) 

⇒ b2 = (a2 – c2) = 122 – 42 = 128

Hence, the equation of the ellipse is

x2/144 + y2/128 = 1.

Question 3: 

For a given hyperbola x2/36 – y2/64 = 1. Find the following:

(i) length of the axes;

(ii) coordinates of vertices and foci;

(iii) the eccentricity;

(iv) length of the latus rectum.

Solution:

Comparing the given equation of hyperbola to the standard equation x2/a2 – y2/b2 = 1, we get a2 = 36 and b2 = 64. 

∴ a = 6, b = 8 and c = (a2 + b2)½ = (36 + 64)½  = 10.

Length of axes	Length of transverse axis = 2a = 12 units Length of conjugate axis = 2b = 16 units
Coordinates of vertices	A( –a, 0) and B(a, 0), that is, A( –6, 0) and B(6, 0)
Coordinates of foci	F1( –c, 0) and F2(c, 0), that is, F1( –10, 0) and F2(10, 0)
Eccentricity	e = c/a = 10/6 = 5/3
Length of latus rectum	2b2/a = (2 × 82)/6 = 64/3 unit