Subtraction

Subtraction is one of the four basic arithmetic operations in mathematics. We can observe the applications of subtraction in our everyday life in different situations. For example, when we purchase fruits and vegetables for a certain amount of money say Rs. 150 and we have given a Rs. 200 note to the vendor. Now, the vendor returns the excess amount by performing subtraction such as 200 – 150 = 50. Then, the vendor will return Rs. 50.

In this article, you will learn the meaning and definition of subtraction in maths, the symbol for subtraction, rules, how to subtract numbers in different ways such as subtraction of numbers on the number line along with examples and properties of subtraction.

Subtraction Meaning

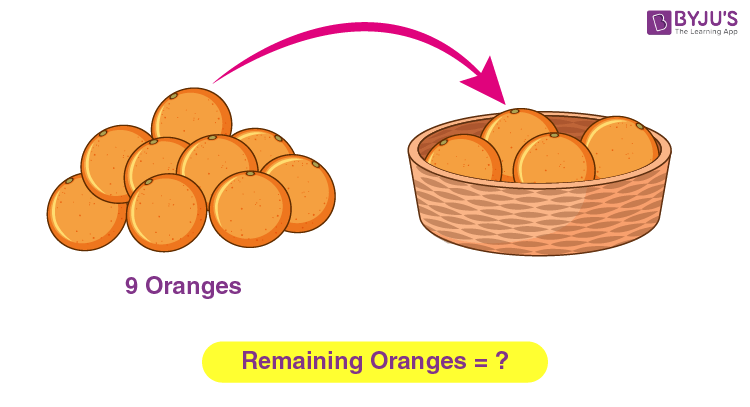
Subtraction represents the operation of removing objects from a collection. The minus sign signifies subtraction −. For example, there are nine oranges arranged as a stack (as shown in the above figure), out of which four oranges are transferred to a basket, then there will be 9 – 4 oranges left in the stack, i.e. five oranges. Therefore, the difference between 9 and 4 is 5, i.e., 9 − 4 = 5. Subtraction is not only applied to natural numbers but also can be incorporated for different types of numbers. That means we can also describe decreasing or removing physical and abstract quantities with various sets of objects such as negative numbers, fractions, rational & irrational numbers, decimals, functions, matrices and vectors.

Subtraction Symbol and Parts

The symbol “-” signifies subtraction. A subtraction process consists of three parts of numbers, namely minuend, subtrahend and difference. The number in a subtraction sentence from which we subtract another number is called a minuend, which means the minuend is the first number in a subtraction process.

Example: 8 – 6 = 2

Here,

8 = Minuend

6 = Subtrahend

2 = Difference

And, “-” is the minus, i.e. the symbol for subtraction and “=” is the equal sign.

However, the parts of the subtraction can be shown as:

Subtraction Table

Let’s have a look at the subtraction table of simple subtractions of numbers.

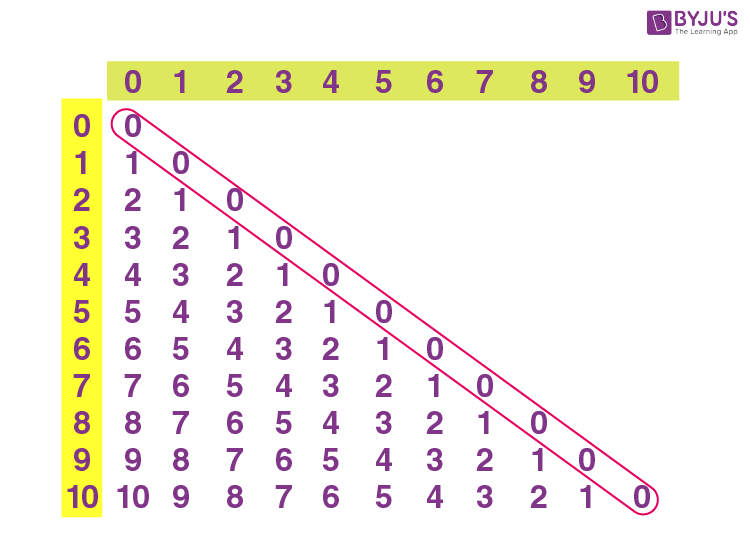
Here, we can observe that the subtraction of equal numbers always results in 0, i.e. 2 – 2 = 0, 3 – 3 = 0 and so on.

Subtraction sums

Subtraction can be performed on single-digit, double-digit, triple-digit numbers and so on. Single-digit subtraction is quite simple as shown in the below examples.

Single digit subtraction:

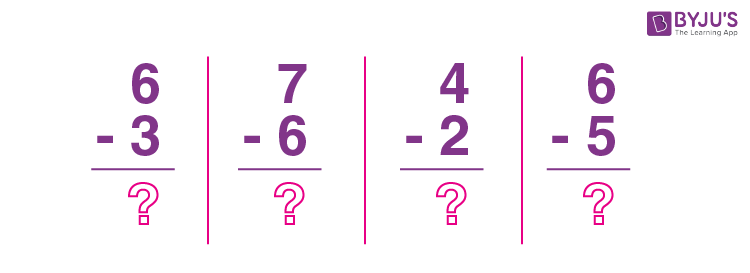
Here, 6 – 3 = 3, 7 – 6 = 1, 4 – 2 = 2 and 6 – 5 = 1.

Subtraction of a single digit from a two-digit number:

In this case, subtraction of digits may involve borrowing from the adjacent digit.

Consider the second sum from the above figure.

70 – 5; here first we have to perform subtraction for unit digits, i.e. for 0 and 5.

0 is less than 5 hence we have to borrow 1 from the adjacent digit, i.e. we have to take 1 from 7 so that 7 will become 6 and 0 will become 10.

Now, 10 -5 = 5 and the leftover digit is 6. Therefore, 70 – 5 = 65.

Subtraction of two digit numbers:

Here, 78 – 18 = 60

85 – 75 = 10

68 – 47 = 21

70 – 41 = 29

Similarly, we can subtract two-digit or three-digit numbers from three-digit numbers. Large numbers can also be subtracted from each other.

Subtraction of Fractions

Subtraction of fractions can be done depending on the types of fractions given. This can be done as follows.

• If the given fractions are like fractions, then subtract the numerators and keep the denominator as it is. Then simplify the fraction if possible to get the result.
• If the given fractions are unlike fractions, then convert them into like fractions and follow the procedure as mentioned above.

Examples:

• (7/9) – (4/9) = (7 – 4)/9 = 3/9 = ⅓
• (5/6) – (2/3)
  Here, 2/3 ⇒ (2/3) × (2/2) = 4/6
  Now, (5/6) – (2/3) = (5/6) – (4/6) = 1/6

Subtraction of Integers

The subtraction of integers involves three possibilities such as:

• Subtraction between two positive numbers
• Subtraction between two negative numbers
• Subtraction between a positive number and a negative number

For easy computation, we have to convert the subtraction problems into additional problems. This contains two steps as given below:

Step 1: Convert the subtraction sign into an addition sign.

Step 2: After converting the sign, take the inverse of the number which comes after the sign.

The properties of subtraction of integers are tabulated below.

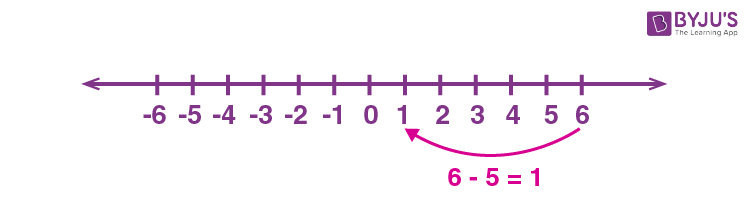
Subtraction on Number line

Let us consider the below example to understand the subtraction of numbers on the number line.

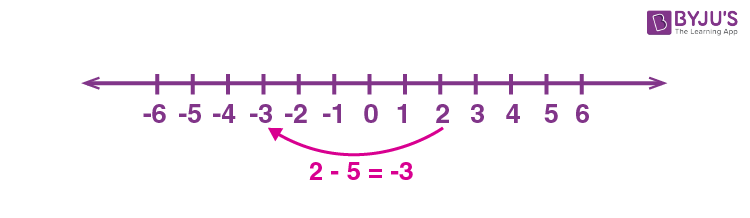
Here, subtraction of 5 from 2 gives -3.

Consider another example 6 – 5:

Subtraction word problems

An important key for solving word problems on subtraction is given below.

Few words such as “minus, difference, less, deduct, take away, decrease” often represent subtraction.

Example 1:

Suma has 12 pens. Her friend Jessi has 5 pens less than Suma. How many pens does Jessi have?

Solution:

As we know, the term “less than” refers to the incorporation of subtraction.

Given,

Suma = 12

Jessi = 12 – 5 = 7

Therefore, Jessi has 7 pens.

Example 2:

By how much is 3576 less than 5344?

Solution:

From the given, it is clear that 5344 is greater than 3576.

Now subtract 3576 from 5344.

5344 – 3576 = 1768

Therefore, 3576 is less than 5344 by 1768.

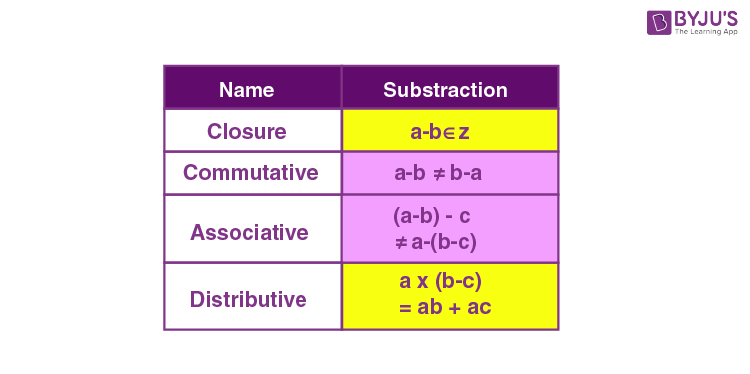
Subtraction Properties

Subtraction of numbers possess some properties as given below:

• We can transform any subtraction problem into a problem with addition and vice-versa.
• Subtracting 0 from any number gives the number itself, i.e. the difference is nothing.
• When we subtract 1 from any number, the difference always equals the predecessor of the number.
• The subtraction of numbers is anti-commutative.
• Subtraction of numbers is non-associative.

&

Win