We know that momentum is a vector quantity that can be conserved. Momentum is defined as the product of the mass of a particle and its velocity. This article lets us know more about the conservation of momentum, along with its examples.
What Is Conservation Of Momentum?
Conservation of momentum is a major law of physics which states that the momentum of a system is constant if no external forces are acting on the system. It is embodied in Newton’s First Law or The Law of Inertia.
The law of conservation of momentum is generously confirmed by experiment and can even be mathematically deduced on the reasonable presumption that space is uniform.
Conservation of Linear Momentum:
Conservation of linear momentum is based on Newton’s second law of motion, which states that in an isolated system, the total momentum remains the same. Let’s consider the following example,
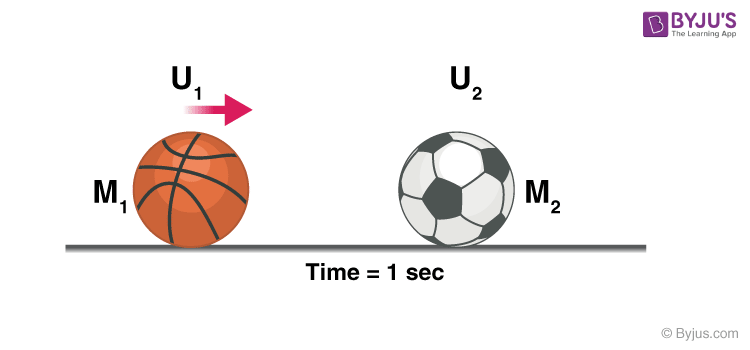
Remember: In the above experiment, we did not consider any loss of energy due to friction, heat, etc. and all the collisions were elastic in nature, i.e. there was a total transfer of energy, actual observations may differ.
Let’s consider a case where a football of mass M2 is resting on the ground, and a bowling ball with a comparatively heavier mass of M1 is thrown at the football at a velocity of U1.
When the bowling ball hits the football the energy is transferred and the bowling ball loses some velocity and moves at a new velocity V1, the football moves at velocity V2, why did the football move?

To conserve linear momentum, i.e. the bowling ball had an initial momentum of M1 so as M2 < M1 and the momentum of football should be equal to the momentum lost by the bowling ball according to the law of conservation of momentum, the football had no other option than moving at a velocity V2.
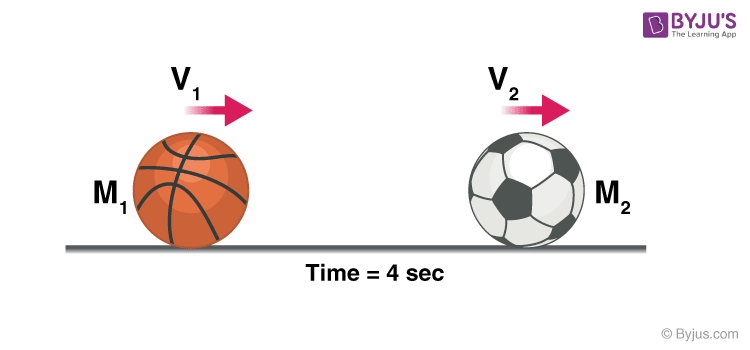
Formula:
Where,
m1 is mass of the bowling ball
m2 is the mass of the football
u1 and u2 are the initial velocities and v1 and v2 are the final velocities.
Even though the momentum of each particle changes, altogether the momentum of the system remains constant as long as there is no external force acting on it. In a head-to-head car accident, the momentum is transferred from one car to the other, but so much force is applied that the car structure cannot handle it, this is why a car wrecks. If the cars were able to deal with the amount of force, and the collision was elastic they both will move in opposite directions, considering their weights are the same.
In short, momentum is always conserved in any collision, whether it be an elastic or a non-elastic collision, though kinetic energy is not conserved in a non-elastic collision, the kinetic energy is converted into heat energy or potential energy, etc.
Example of Conservation of Momentum
Consider this example of a balloon, the particles of gas move rapidly colliding with each other and the walls of the balloon, even though the particles themselves move faster and slower when they lose or gain momentum when they collide, the total momentum of the system remains the same.

Hence, the balloon doesn’t change in size, if we add external energy by heating it, the balloon should expand because it increases the velocity of the particles and this increases their momentum, in turn, increasing the force exerted by them on the walls of the balloon.
Application of Law of Conservation of Momentum
Having said so the energy of a system is always conserved, one of the best applications of the law of conservation of momentum would be in space travel, there is no medium in space to exert a force on, then how do rockets travel?

Well, they eject matter at a very high speed, so in an isolated system, the momentum should remain constant therefore, the rocket will move in the opposite direction with the same momentum as that of the exhaust.
What is Conservation of Angular Momentum?
It is the rotational analog of linear momentum, it is denoted by l, and angular momentum of a particle in rotational motion is defined as:
This is a cross product of r ,i.e. the radius of the circle formed by the body in rotational motion, and p, i.e. the linear momentum of the body, the magnitude of a cross product of two vectors is always the product of their magnitude multiplied with the sine of the angle between them, therefore in the case of angular momentum the magnitude is given by,
Torque and Angular Momentum Relationship
Relationship between torque and angular momentum can found as follows,
Conservation of Angular Momentum – Calculation
Angular momentum of a system is conserved as long as there is no net external torque acting on the system, the earth has been rotating on its axis from the time the solar system was formed due to the law of conservation of angular momentum,
There are two ways to calculate the angular momentum of any object, if it is a point object in a rotation, then our angular momentum is equal to the radius times the linear momentum of the object,
Now when we somehow decrease the radius of the ball by shortening the string while it is in rotation, the r will reduce, now according to the law of conservation of angular momentum L should remain the same, there is no way for mass to change, therefore vector v should increase, to keep the angular momentum constant, this is the proof for the conservation of angular momentum.
Conservation of Angular Momentum Applications
Law of conservation of angular momentum has many applications, including:
- Electric generators,
- Aircraft engines, etc.












0 Comments