Inverse Trigonometric Functions

Inverse trigonometric functions are defined as the inverse functions of the basic trigonometric functions, which are sine, cosine, tangent, cotangent, secant and cosecant functions. They are also termed arcus functions, antitrigonometric functions or cyclometric functions. These inverse functions in trigonometry are used to get the angle with any of the trigonometry ratios. The inverse trigonometry functions have major applications in the field of engineering, physics, geometry and navigation.

What Are Inverse Trigonometric Functions?

Inverse trigonometric functions are also called “arc functions” since, for a given value of trigonometric functions, they produce the length of arc needed to obtain that particular value. The inverse trigonometric functions perform the opposite operation of the trigonometric functions such as sine, cosine, tangent, cosecant, secant and cotangent. We know that trigonometric functions are applicable, especially to the right-angle triangle. These six important functions are used to find the angle measure in the right-angle triangle when two sides of the triangle measures are known.

Formulas

The basic inverse trigonometric formulas are as follows:

Inverse Trig Functions	Formulas
Arcsine	sin-1(-x) = -sin-1(x), x ∈ [-1, 1]
Arccosine	cos-1(-x) = π -cos-1(x), x ∈ [-1, 1]
Arctangent	tan-1(-x) = -tan-1(x), x ∈ R
Arccotangent	cot-1(-x) = π – cot-1(x), x ∈ R
Arcsecant	sec-1(-x) = π -sec-1(x), |x| ≥ 1
Arccosecant	cosec-1(-x) = -cosec-1(x), |x| ≥ 1

Inverse Trigonometric  Functions Graphs

There are particularly six inverse trig functions for each trigonometry ratio. The inverse of six important trigonometric functions are

• Arcsine
• Arccosine
• Arctangent
• Arccotangent
• Arcsecant
• Arccosecant

Let us discuss all six important types of inverse trigonometric functions, along with its definition, formulas, graphs, properties and solved examples.

Arcsine Function

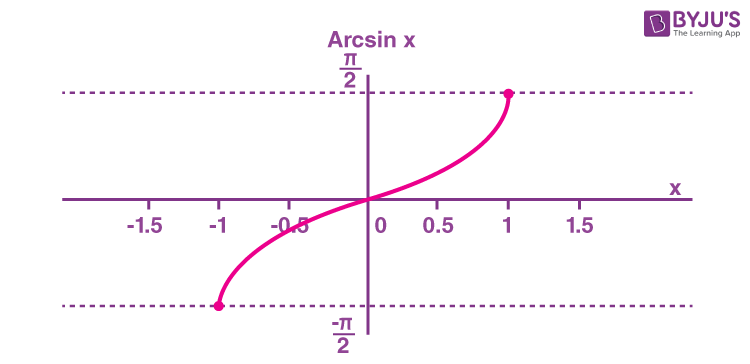
The arcsine function is an inverse of the sine function denoted by sin-1x. It is represented in the graph as shown below.

Domain	-1 ≤ x ≤ 1
Range	-π/2 ≤ y ≤ π/2

Arccosine Function

The arccosine function is the inverse of the cosine function denoted by cos-1x. It is represented in the graph as shown below.

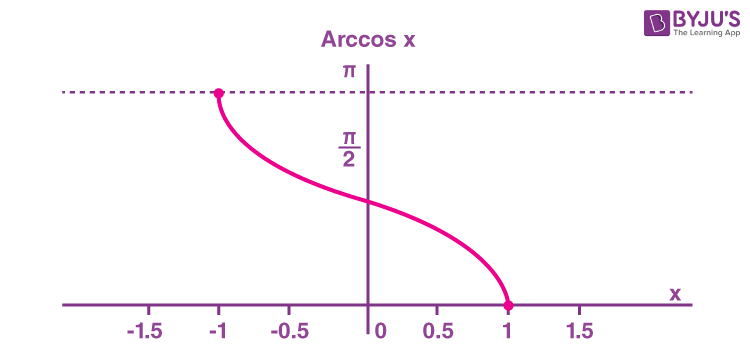
Therefore, the inverse of the cos function can be expressed as y = cos-1x (arccosine x)

Domain and range of arcsine function are as follows:

Domain	-1≤x≤1
Range	0 ≤ y ≤ π

Arctangent Function

The arctangent function is the inverse of the tangent function denoted by tan-1x. It is represented in the graph as shown below.

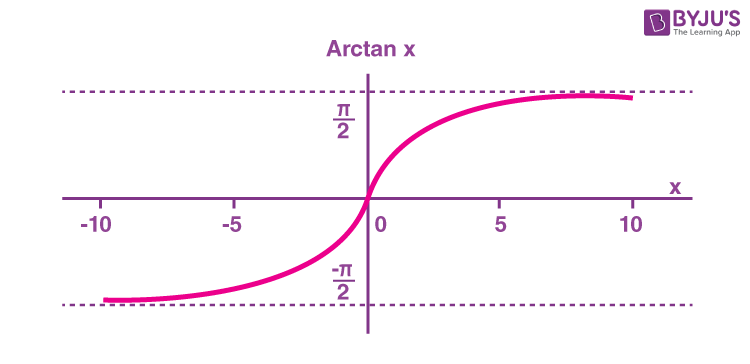
Therefore, the inverse of the tangent function can be expressed as y = tan-1x (arctangent x)

Domain and range of arctangent are as follows:

Domain	-∞ < x < ∞
Range	-π/2 < y < π/2

Arccotangent (Arccot) Function

The arccotangent function is the inverse of the cotangent function denoted by cot-1x.

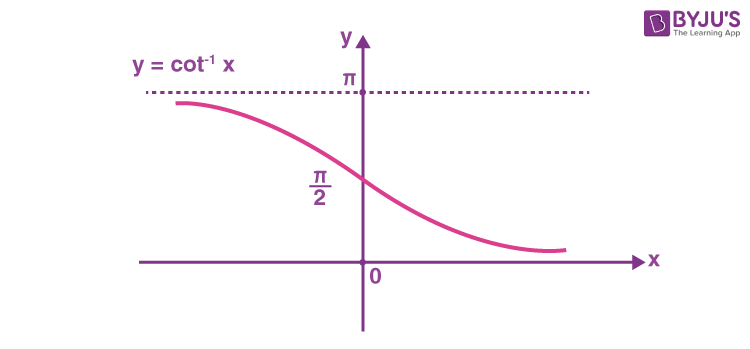
Therefore, the inverse of the cotangent function can be expressed as y = cot-1x (arccotangent x)

Domain and range of arccotangent are as follows:

Domain	-∞ < x < ∞
Range	0 < y < π

Arcsecant Function

What is the arcsecant (arcsec) function? The arcsecant function is the inverse of the secant function denoted by sec-1x. It is represented in the graph as shown below.

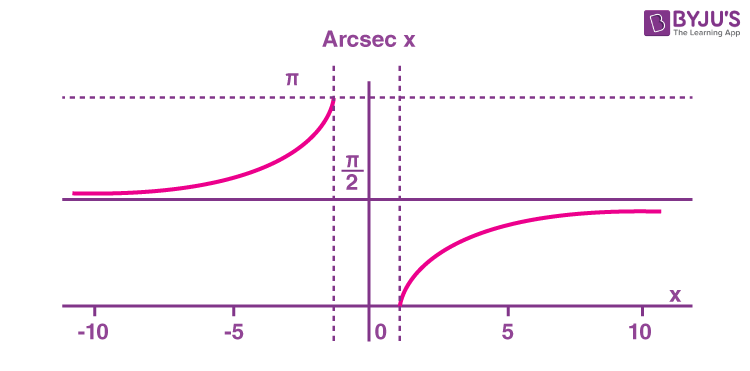
Therefore, the inverse of the secant function can be expressed as y = sec-1x (arcsecant x)

Domain and range of arcsecant are as follows:

Domain	-∞ ≤ x ≤ -1 or 1 ≤ x ≤ ∞
Range	0 ≤ y ≤ π, y ≠ π/2

Arccosecant Function

What is the arccosecant (arccsc x) function? The arccosecant function is the inverse of the cosecant function denoted by cosec-1x. It is represented in the graph as shown below.

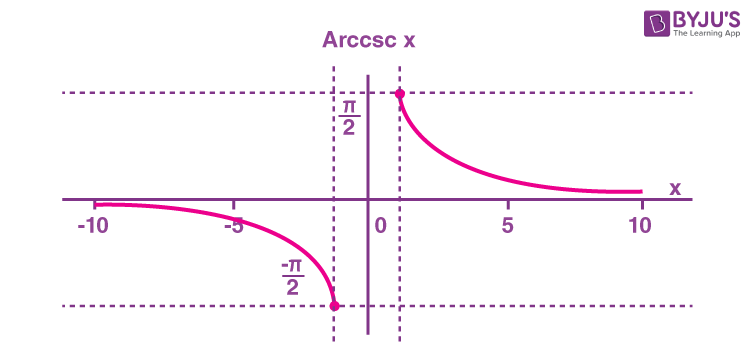
Therefore, the inverse of the cosecant function can be expressed as y = cosec-1x (arccosecant x)

Domain and range of arccosecant are:

Domain	-∞ ≤ x ≤ -1 or 1 ≤ x ≤ ∞
Range	-π/2 ≤ y ≤ π/2, y ≠ 0

Inverse Trigonometric Functions Table

Let us look at all the inverse trigonometric functions with their notation, definition, domain and range.

Function Name	Notation	Definition	Domain of  x	Range
Arcsine or inverse sine	y = sin-1(x)	x=sin y	−1 ≤ x ≤ 1	− π/2 ≤ y ≤ π/2 -90°≤ y ≤ 90°
Arccosine or inverse cosine	y=cos-1(x)	x=cos y	−1 ≤ x ≤ 1	0 ≤ y ≤ π 0° ≤ y ≤ 180°
Arctangent or inverse tangent	y=tan-1(x)	x=tan y	For all real numbers	− π/2 < y < π/2 -90°< y < 90°
Arccotangent or inverse cot	y=cot-1(x)	x=cot y	For all real numbers	0 < y < π 0° < y < 180°
Arcsecant or inverse secant	y = sec-1(x)	x=sec y	x ≤ −1 or 1 ≤ x	0≤y<π/2 or π/2<y≤π 0°≤y<90° or 90°<y≤180°
Arccosecant	y=csc-1(x)	x=csc y	x ≤ −1 or 1 ≤ x	−π/2≤y<0 or 0<y≤π/2 −90°≤y<0°or 0°<y≤90°

Inverse Trigonometric Functions Derivatives

The derivatives of inverse trigonometric functions are first-order derivatives. Let us check out the derivatives of all six inverse functions here.

Inverse Trig Function	dy/dx
y = sin-1(x)	1/√(1-x2)
y = cos-1(x)	-1/√(1-x2)
y = tan-1(x)	1/(1+x2)
y = cot-1(x)	-1/(1+x2)
y = sec-1(x)	1/[|x|√(x2-1)]
y = csc-1(x)	-1/[|x|√(x2-1)]

Inverse Trigonometric Functions Properties

The inverse trigonometric functions are also known as arc functions. Inverse trigonometric functions are defined in a certain interval (under restricted domains). 

Trigonometry Basics

Trigonometry basics include the basic trigonometry and trigonometric ratios, such as sin x, cos x, tan x, cosec x, sec x and cot x.

Inverse Trigonometric Functions Problems

Example 1: Find the value of x for sin(x) = 2.

Solution: Given: sin x = 2

x =sin-1(2), which is not possible.

Hence, there is no value of x for which sin x = 2, so the domain of sin-1x is -1 to 1 for the values of x.

Example 2: Find the value of sin-1(sin (π/6)).

Solution:

sin-1(sin (π/6) = π/6 (Using identity sin-1(sin (x) ) = x)

Example 3: Find sin (cos-1 3/5).

Solution:

Suppose that, cos-1 3/5 = x

So, cos x = 3/5

\(\begin{array}{l}We\ know,\ sin\  x = \sqrt{1 – cos^2 x}\end{array} \)

\(\begin{array}{l}So,\ sin\ x = \sqrt{1 – \frac{9}{25}}= \frac{4}{5}\end{array} \)

This implies, sin x = sin (cos-1 3/5) = 4/5

Example 4: 

\(\begin{array}{l}Solve:\sin ({{\cot }^{-1}}x)\end{array} \)

Solution:

\(\begin{array}{l}Let\ {{\cot }^{-1}}x=\theta \,\,\Rightarrow \,\,x=\cot \theta\end{array} \)

\(\begin{array}{l}Now, \ \cos ec\,\theta =\sqrt{1+{{\cot }^{2}}\theta }=\sqrt{1+{{x}^{2}}}\end{array} \)

\(\begin{array}{l}Therefore,\ \sin \theta =\frac{1}{\cos ec\,\theta }=\frac{1}{\sqrt{1+{{x}^{2}}}}\,\,\Rightarrow \,\theta ={{\sin }^{-1}}\frac{1}{\sqrt{1+{{x}^{2}}}}\end{array} \)

\(\begin{array}{l}Hence, \sin \,({{\cot }^{-1}}x)\,=\sin \,\left( {{\sin }^{-1}}\frac{1}{\sqrt{1+{{x}^{2}}}} \right) =\frac{1}{\sqrt{1+{{x}^{2}}}}={{(1+{{x}^{2}})}^{-1/2}}\end{array} \)

Example 5:

\(\begin{array}{l}Solve:{{\sec }^{-1}}[\sec (-{{30}^{o}})]\end{array} \)

Solution: 

\(\begin{array}{l}{{\sec }^{-1}}[\sec \,(-{{30}^{o}})]={{\sec }^{-1}}(\sec {{30}^{o}})={{30}^{o}}\end{array} \)

Example 6:

\(\begin{array}{l}If~ sin \left( {{\sin }^{-1}}\frac{1}{5}+{{\cos }^{-1}}x \right)=1,\ then\ what\ is\ the\ value\ of\ x?\end{array} \)

Solution:

\(\begin{array}{l}{{\sin }^{-1}}\frac{1}{5}+{{\cos }^{-1}}x=\frac{\pi }{2}\\ {{\sin }^{-1}}\frac{1}{5}=\frac{\pi }{2}-{{\cos }^{-1}}x={{\sin }^{-1}x}\\ x=\frac{1}{5}\end{array} \)

&

Win