Ohm’s law states the relationship between electric current and potential difference. The current that flows through most conductors is directly proportional to the voltage applied to it. Georg Simon Ohm, a German physicist was the first to verify Ohm’s law experimentally.
Ohm’s Law Explanation

One of the most basic and important laws of electric circuits is Ohm’s law.
Ohm’s law states that the voltage across a conductor is directly proportional to the current flowing through it, provided all physical conditions and temperatures remain constant.
Mathematically, this current-voltage relationship is written as,

In the equation, the constant of proportionality, R, is called Resistance and has units of ohms, with the symbol Ω.
The same formula can be rewritten in order to calculate the current and resistance respectively as follows:


Ohm’s law only holds true if the provided temperature and the other physical factors remain constant. In certain components, increasing the current raises the temperature. An example of this is the filament of a light bulb, in which the temperature rises as the current is increased. In this case, Ohm’s law cannot be applied. The lightbulb filament violates Ohm’s Law.
| Ohm’s Law Statement: Ohm’s law states that the voltage across a conductor is directly proportional to the current flowing through it, provided all physical conditions and temperature, remain constant. Ohm’s Law Equation: V = IR, where V is the voltage across the conductor, I is the current flowing through the conductor and R is the resistance provided by the conductor to the flow of current. |
Relationship Between Voltage, Current and Resistance
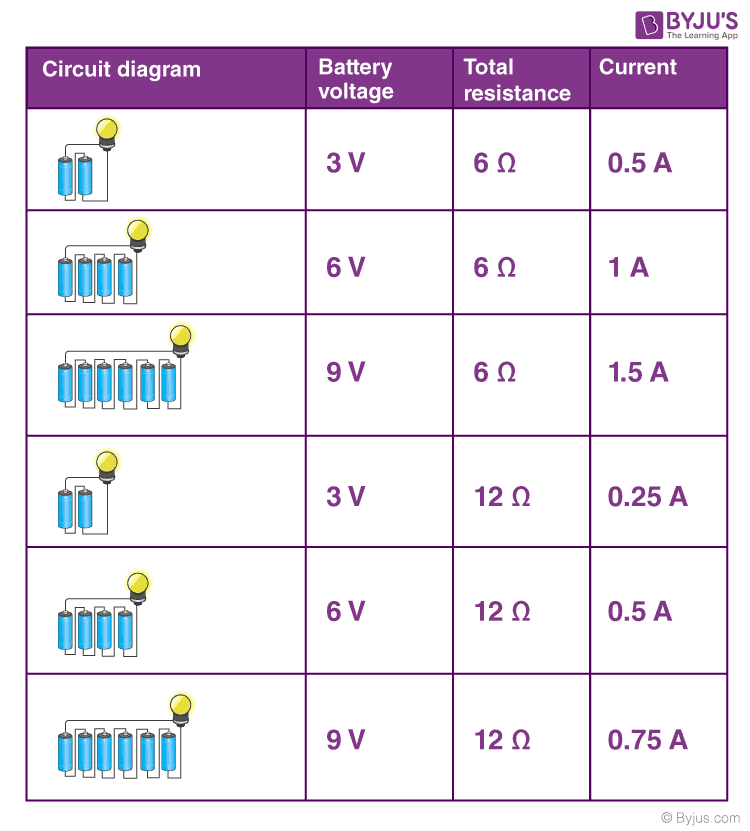
Analyzing rows 1, 2 and 3, we come to understand that doubling and tripling the voltage leads to doubling and a tripling of the current in the circuit. Likewise, when we compare rows 1 and 4 and rows 2 and 5, we come to understand that doubling the total resistance serves to halve the current in the circuit.
Water Pipe Analogy for Ohm’s Law
Ohm’s Law describes the current flow through a resistance when different electric potentials (voltage) are applied at each end of the resistance. Since we can’t see electrons, the water-pipe analogy helps us understand the electric circuits better. Water flowing through pipes is a good mechanical system that is analogous to an electrical circuit.

Here, the voltage is analogous to water pressure, the current is the amount of water flowing through the pipe, and the resistance is the size of the pipe. More water will flow through the pipe (current) when more pressure is applied (voltage) and the bigger the pipe (lower the resistance).
The video below shows the physical demonstration of the Waterpipe analogy and explains to you the factors that affect the flow of current
Experimental Verification of Ohm’s Law
Ohm’s Law can be easily verified by the following experiment:
Apparatus Required:
- Resistor
- Ammeter
- Voltmeter
- Battery
- Plug Key
- Rheostat
Circuit Diagram:
Procedure:
- Initially, the key K is closed and the rheostat is adjusted to get the minimum reading in ammeter A and voltmeter V.
- The current in the circuit is increased gradually by moving the sliding terminal of the rheostat. During the process, the current flowing in the circuit and the corresponding value of potential difference across the resistance wire R are recorded.
- This way different sets of values of voltage and current are obtained.
- For each set of values of V and I, the ratio of V/I is calculated.
- When you calculate the ratio V/I for each case, you will come to notice that it is almost the same. So V/I = R, which is a constant.
- Plot a graph of the current against the potential difference, it will be a straight line. This shows that the current is proportional to the potential difference.
Similar Reading:
Ohm’s Law Magic Triangle
You can make use of Ohm’s law magic triangle to remember the different equations for Ohm’s law used to solve for different variables(V, I, R).
If the value of voltage is asked and the values of the current and resistance are given, then to calculate voltage simply cover V at the top. So, we are left with the I and R or I × R. So, the equation for Voltage is Current multiplied by Resistance. Examples of how the magic triangle is employed to determine the voltage using Ohm’s law are given below.
Ohm’s Law Solved Problems
Example 1: If the resistance of an electric iron is 50 Ω and a current of 3.2 A flows through the resistance. Find the voltage between two points.
Solution:
If we are asked to calculate the value of voltage with the value of current and resistance, then cover V in the triangle. Now, we are left with I and R or more precisely I × R.
Therefore, we use the following formula to calculate the value of V:
V = I × R
Substituting the values in the equation, we get
V = 3.2 A × 50 Ω = 160 V
| V = 160V |
Example 2: An EMF source of 8.0 V is connected to a purely resistive electrical appliance (a light bulb). An electric current of 2.0 A flows through it. Consider the conducting wires to be resistance-free. Calculate the resistance offered by the electrical appliance.
Solution:
When we are asked to determine the value of resistance when the values of voltage and current are given, we cover R in the triangle. This leaves us with only V and I, more precisely V ÷ I.
Substituting the values in the equation, we get
R = V ÷ I
R = 8 V ÷ 2 A = 4 Ω
| R = 4 Ω |
Calculating Electrical Power Using Ohm’s Law
The rate at which energy is converted from the electrical energy of the moving charges to some other form of energy like mechanical energy, heat energy, energy stored in magnetic fields or electric fields, is known as electric power. The unit of power is the watt. The electrical power can be calculated using Ohm’s law and by substituting the values of voltage, current and resistance.
Formula to find power
When the values for voltage and current are given,
When the values for voltage and resistance are given,
When the values for current and resistance are given,
What is a Power Triangle?

The power triangle can be employed to determine the value of electric power, voltage and current when the values of the other two parameters are given to us. In the power triangle, the power (P) is on the top and current (I) and voltage (V) are at the bottom.
When the values of current and voltage are given, the formula for finding power is,
When the values of power and voltage are given, the formula for finding current is,
When the values of power and current are given, the formula for finding voltage is,
Ohm’s Law Pie Chart
To better understand the relationship between various parameters, we can take all the equations used to find the voltage, current, resistance and power, and condense them into a simple Ohm’s Law pie chart as shown below.
Ohm’s Law Matrix Table
Like Ohm’s Law Pie Chart shown above, we can condense the individual Ohm’s Law equations into a simple matrix table as shown below for easy reference when calculating an unknown value.
Ohm’s Law Applications
The main applications of Ohm’s law are:
- To determine the voltage, resistance or current of an electric circuit.
- Ohm’s law maintains the desired voltage drop across the electronic components.
- Ohm’s law is also used in DC ammeter and other DC shunts to divert the current.
Limitations of Ohm’s Law
Following are the limitations of Ohm’s law:
- Ohm’s law is not applicable for unilateral electrical elements like diodes and transistors as they allow the current to flow through in one direction only.
- For non-linear electrical elements with parameters like capacitance, resistance etc the ratio ofvoltage and current won’t be constant with respect to time making it difficult to use Ohm’s law.
Ohm’s law is one of the most popular and important laws that helps us define the relationship between voltage, current and resistance. The law was first established by a German physicist named Georg Simon Ohm, and was the most important theory to describe the quantitative characteristics of the physics of electricity.
Ohm’s law can be also be considered as an empirical law. It can be used in developing conclusions or in reasoning while conducting many experiments, especially in showing that current for some materials is approximately proportional to the electric field. We shall learn more about this law including its definition, formulas, applications and more in this lesson.
What Is Ohm’s Law?
Ohm’s law states that the current through a conductor between two points is directly proportional to the voltage across the two points.
Ohm’s law formula is written as;
V ∝ I
Therefore, V = RI where R is a constant called resistance. R depends on the dimensions of the conductor and also on the material of the conductor. Its SI unit is Ohm (Ω).

Ohm’s law was found out by various experiments, somewhat similar to the thermodynamic laws. As far as its significance is concerned, this law is used within all branches of electronic studies or science. The law is useful in carrying out calculations such as in determining the value of resistors or the current in a circuit or in measuring voltage.
Additionally, Ohm’s law helps us describe how current flows through materials such as electrical wires, etc.
Ohm’s Law Formulas
There are basically three types of Ohm’s law formulas or equations. They are;
- I = V / R
- V = IR
- R = V / I
Here, I is the resistance, V is voltage and R is resistance.
Ohm’s Law Triangle
Ohm’s law is often used in the study of electronics and electricity. Therefore, it is crucial for students to remember the formulas as it will help in circuit analysis. Ohm’s law formulas given above can be easily remembered using the Ohm’s law triangle. This triangle helps us to easily represent the interchangeability of the equations. We can take a triangle and divide it into three parts. Then we can input the values, V, I, R into the triangle. V on top, I on the left side and R on the right side. It will look like this;

Whenever you want to solve the calculation you can just cover the value you are looking for.
Vector Form of Ohm’s Law
The vector form of Ohm’s law is used in electromagnetics and material science. The vector form is given as,
Where,
– represents vector
Conductivity is the reciprocal of resistivity. Which brings us to the next question, what is resistivity?
Resistivity
Consider a conductor with a cross-sectional area ‘a’ and length ‘l’. Let its resistance be R. Let it have a voltage difference of V volts between its end and a current I flowing through it.
Now consider another conductor of the same dimensions, except its length is doubled. This can be considered as two conductors of the first kind connected in series. Therefore, their voltages add up. The voltage here will, therefore, become 2V.
From Ohm’s law, R = (V/T)
Here, R = (2V / I) = 2R
That means that resistance increased with length. That is R ∝ l
Concept point: This does make sense if you think about it. If the length increases, then the flowing electrons will face more obstacles, and hence resistance increases.
Similarly, now consider a conductor with half the cross-sectional area as the first conductor. This can be considered as one of the two conductors in a parallel connection. Therefore, the current becomes half of the original value I/2. Thus, the value of the current becomes I/2 now.
Here, R = (V/ (I/2)) = 2R
This means that resistance increases when the area of cross-section decreases. That is,
R ∝ 1/A
Concept point: As the area of cross-section decreases the flowing electrons come into more contact with positive nuclei of metals. Thus, resistance increases.
Combining these two results we get,
R ∝ l/A
Or, R = ρl / A where ρ is a constant called the coefficient of resistance or resistivity.
In the above equation if L = 1m and A = 1m2, then R = ρ.
This signifies that resistivity is the resistance of a conductor with 1m length and 1m2 area. The resistivity of a conductor is dependent on the nature of its material and certain external factors, such as heat.
Vector Expression
V = IR
⇒ V = I ρL/A
⇒ V = L ρI/A
⇒ V = JρL since current density J = I/A
⇒ El = JρL since V = El
Cancelling L from both sides, E = Jρ or J = E/ρ
1/ρ = σ which is conductivity.
Therefore, = σ where the bar letters are vectors.
Concept point: You might be wondering why current is a scalar unit while current density is a vector unit. To understand this, you need to remember how a vector is defined. A vector is a quantity with both magnitude and direction that obeys the laws of vector addition. The current does not follow the rules of vector addition and hence, it is not a vector.
The broader aspect of this concept that you need to understand here is that vector quantities are concepts we use to aid our calculations. However, sometimes we have to make exceptions in order to make our calculations easier or even correct in some cases.
Ohm’s Law Limitations
There are some limitations to Ohm’s law. They are as follows:
- Ohm’s law is an empirical law which is found true for maximum experiments but not for all.
- Some materials are non-ohmic under a weak electric field.
- Ohm’s law holds true only for a conductor at a constant temperature. Resistivity changes with temperature.
Joules heat is given by H = I2Rt where I is current, R is resistance and t is time. As long as the current flows, greater will be the temperature of the conductor.
- Ohm’s law is not applicable to in-network circuits.
- Ohm’s does not apply directly to capacitor circuits and inductor circuits.
- The V-I characteristics of diodes are different.

- V-I graph of ohmic conductors is not really a straight graph. It does show some variation.

Applications of Ohm’s Law
Ohm’s law is very useful and has several applications. A few are listed below:
- It is widely used in circuit analysis.
- It is used in ammeter, multimeter, etc.
- It is used to design resistors.
- It is used to get the desired circuit drop in circuit design.
- Advanced laws such as Kirchhoff’s Norton’s law, Thevenin’s law are based on Ohm’s law.
- Electric heaters, kettles and other types of equipment working principle follow Ohm’s law.
- A laptop and mobile charger using DC power supply in operation and working principle of DC power supply depend on Ohm’s law.
Ohm’s law also has many other uses as well.
Analogies of Ohm’s Law
Some analogies of Ohm’s law:
Hydraulic Analogy
A hydraulic circuit can be compared to an ohmic conductor to make the problem easier to solve. Here, pressure works similar to voltage and flow rate works similar to current.
Temperature Analogy
Similarly, a temperature circuit can also be compared to an ohmic conductor. Here, temperature gradient works similar to voltage and heat flow works similar to current.
In fact, GS Ohm discovered Ohm’s law by drawing an analogy from Fourier’s work on heat flow.
Related Terms: Current, Voltage and Resistance
Apart from the standard definitions, you need to know what these terms actually mean. Let’s take a look at the current first. Electric current to be more precise. What comes to your mind when you first hear the word current? Perhaps a river that is flowing. That’s what electric current is, it can be visualised as the flow of electrons from one place to another.
Now, why does the flow occur? Well, a river flows from the mountains to the sea, i.e., from a high place to a low place. Well, similarly current flows from a high potential to a low potential, and this change of potential is called voltage.
You may notice that every river has some obstructions and that’s what resistance is to current. Resistance is the property of the conductor that obstructs the flow of current.
Ohm’s Law Problems with Solutions
1. We have an unknown resistor which dissipates 30 watts power while dropping 15 volts across it. Find the current that is flowing through it.
Solution:
We apply Ohm’s law formula for I,
I = P/V = 30/15 = 2 A
2. Apply Ohm’s law for the following circuits.

Solution:
Applying Ohm’s law on the circuit (a)
I = 3 A
Applying Ohm’s law on the circuit (b)
V = I × R
V = 1 × 13
V = 13 V
Applying Ohm’s law on the circuit (c)
R = 2 Ω
3. How much voltage will be dropped across a 50 kΩ resistance whose current is 300 µA?
Given
R = 50 kΩ = 50 × 103Ω
I = 300 µA = 300 × 10-6 A
Solution:
V = I × R
V = (300 × 10-6) × (50 × 103)
V = 15 V
4. Apply the power (P) formula for the following circuit.

Given:
I = 6 A
V = 30 V
R = 5 Ω
Solution:
Power formula: P = VI or P = I2R or
P = 30 × 6
P = 180 W
5. An electric circuit has a current of 3.00 A flowing through it. Find the potential difference across a resistor, with a resistance of 250 Ω.
Solution:
Using the Ohm’s Law formula:
V = IR = (3.00 A)(250 Ω)
V = 750V
The potential difference across the resistor in the circuit is 750 V.







0 Comments