Work and Energy’, discusses the concept of work, energy and power in detail. In day-to-day life, we consider any useful physical or mental labour as work, but work is defined differently in science. Work done by a force acting on an object is equal to the magnitude of the force multiplied by the distance moved in the direction of the force. Work has only magnitude and no direction. Similarly, we often use the term energy in our daily life; this also has a different definition in science. In physics, energy is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of heat and light.
Work and energy are closely related to each other. Work can also be defined as the transfer of energy. In Physics, for two objects, the work done is defined as the transfer of energy from the first object to the second object. Also, energy is defined as the capacity to do work.
Work is believed to be done by a force when an object experiences displacement parallels to the line of action of the force. It’s an activity that includes force and movement in the direction of the force. The capability for doing work is what the energy is! In this article, let’s learn more about work and energy concept along with principle of work and energy.
Work
Work done on an object is defined as the product of the magnitude of the force acting on the body and the displacement in the direction of the force. W = F.s. The SI unit of force is Newton.
If a force acting on a body causes no displacement, the work done is 0. For example, pushing a wall.
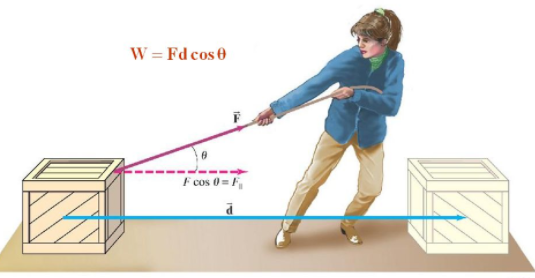
The force component F cos θ gives the component of force along the direction in that the body is displaced. Cos θ is the angle between the force vector and displacement vector.
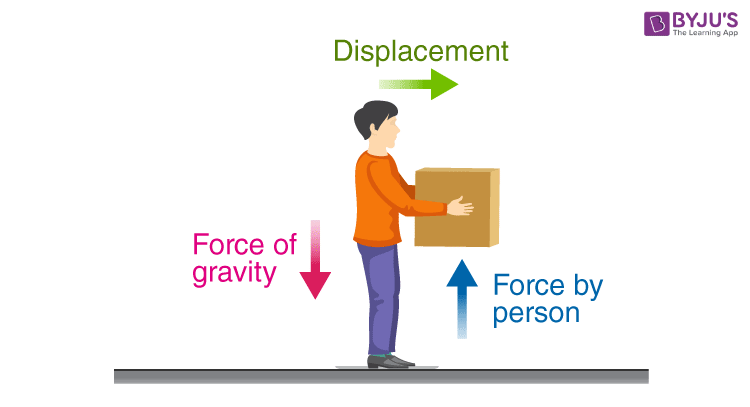
So can there be a situation when force is acting on a body and it is being displaced, but still the work done is zero? Let’s consider the example of a coolie carrying luggage. The force acting on the luggage is a force of gravity, which is vertical and displacement is horizontal. So the displacement in the direction of the force is zero, hence work done by gravity as well as the person is zero.
Similarly, what is the energy when we are pushing a wall? It is very shocking that even though you feel fatigue but work done by you on the wall is zero. The displacement of the wall is zero.
Energy
Energy is defined as the ability to do work. Its unit is the same as that of work. Energy is a scalar quantity.
SI unit of energy or work = Joule (Nm) or Kgm2s−2.
Principle of Work and Energy
The work-energy principle says states that
The change in kinetic energy of a body is equivalent to the net work done on the body.
This information is referred to as the work-energy principle and is derivable from the law conservation of energy.
Here K.Ef is the final kinetic energy and K.Ei is the initial kinetic energy.
Forms of Energy
Energy has different forms: Light, heat, chemical, electrical or mechanical.
Mechanical energy is the sum of
(i) Kinetic energy (K.E)
(ii) Potential energy (P.E)
Kinetic Energy
Objects in motion possess energy and can do work. This energy is called Kinetic Energy.
Also,From the second equation of motion, we know thatRearranging the equation, we getSubstituting equation for work done by a moving body,Taking initial velocity as zero, we getWhen two identical bodies are in motion, the body with a higher velocity has more KE.


Work and Energy Equations
It is the resultant of the force applied (F) and the amount of displacement (d) and is articulated by the equation
W = F.d
Power describes the rate at which work is done. It is articulated as
P = W/t
The energy or work is articulated in Newton-meter (Nm) or Joules or kg.m2/s2. 1 Joule is defined as the amount of heat released when a force of 1 newton acts over one meter of distance.
Ever wondered what happens when the work is done against gravity?
When the work done is against gravity, the amount of work done will be equal to the product of the weight of an object and the height through which the object is lifted.
The mathematical representation of work done against the gravity is given as:
| W = m x g x h |
Where,
- W is the work done
- m is the mass of an object
- g is the acceleration due to gravity
- h is the height through which the object is been lifted
Work-Energy Theorem
The work-energy theorem states that the net work done by a moving body can be calculated by finding the change in KE.
⇒ W net = KE final − KE initial
⇒ Wnet=
m[v2−u2]Factors Affecting Kinetic Energy
- Mass
- Velocity
- Momentum
Potential Energy
Energy can get stored in an object when work is done on it.
For example, stretching a rubber string. The energy that is possessed by a body by virtue of its configuration or change in position is known as Potential Energy.

The potential energy of an object at a height
When an object is raised to a certain height, work is done against gravity to change its position. This energy is stored as Potential Energy.
⇒W = F.s
⇒F = ma
In the case of increasing the height, F = mg
Therefore, W (P.E) = mgh
⇒ ΔPE=mg(h final−h initial)
Law of Conservation of Energy
Law of conservation of energy states that energy can neither be created nor destroyed but can be transferred from one form to another. The total energy before and after the transformation remains constant.
Total energy = KE + PE
where, 1/2 mv2 + mgh = constant
For example: consider a ball falling freely from a height. At height h, it has only PE = mgh.
By the time it is about to hit the ground, it has a velocity and therefore has KE=
mv2. Therefore, energy gets transferred from PE to KE, while the total energy remains the same.





0 Comments